为什么要白化
假设训练数据是图像,由于图像中相邻像素之间具有很强的相关性,所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性。比如在独立成分分析(ICA)中,对数据做白化预处理可以去除各观测信号之间的相关性,从而简化了后续独立分量的提取过程,而且,通常情况下,数据进行白化处理与不对数据进行白化处理相比,算法的收敛性较好。
一些容易与白化变换混淆的概念包括:去相关化、标准化、有色变换。去相关化仅仅使得各个分量之间不相关,而对于整体的方差没有进行考虑。标准化使得整体的方差为1但是没有考虑相关性。有色变换是使得一个白色随机序列根据设计好的相关性矩阵变成一个要求的有色序列。
为什么在白化变换中一定要求白化后的方差为1呢?举个例子,在信号处理中,一个随机信号u通过一个放大率为100的线性放大器得到另一个随机变量w,从方差的角度看其方差变为原来的10000倍,看起来是另一个与u完全不同的信号,但是实际上只是数值按比例放大,比如采用了不同的计量单位来量化同一个物理信号,两个看似不同的信号却描述了同一个物理现象。为了避免这种情况,最好在白化变换中将信号的整体方差也归一化为1,这样就可以避免类似的问题。
白化的两种方式:
- PCA白化
- ZCA白化
白化的定义
“白化”这个词最早来源于信号处理领域,跟其中最常见的一种噪声——白噪声有很大的联系。在信号处理理论中,白噪声指的是一种在不同频率都有相同功率的随机信号,即其功率谱密度为常数,功率与频率无关。“白噪声”这个名字来源于白光,白光包含了光谱中所有的颜色,其功率谱密度也呈平坦状,类似地,“白噪声”这种噪声中包含了所有频率的噪声,因此被冠上了“白”的称号。其他不满足该功率谱密度特性的噪声也被称为有色噪声,类似于非白光的其他颜色光。
简单来说,白色的定性就是均值为0,不相关。明白了白色的内涵之后,“白化”的概念也就很容易理解了,对于一个随机向量,如果它是白化的,那么它满足两个条件:
(1)各分量零均值且方差为1
(2)各分量不相关
通过上面两个条件限制,可以发现白化向量的协方差矩阵为单位矩阵。白化变换的定义为:白化变换或球面变换是一种线性变换,它将具有已知协方差矩阵的随机变量向量转换为一组新变量组成的向量,使得新的向量协方差矩阵为一个单位矩阵。(白化强于不相关的地方在于白化后矩阵的特征方差是1。)
对于零均值这个条件,只需要把原始向量减去均值就可以了:
针对第二个条件,假设 $X$ 是一个均值为0的随机向量,其协方差矩阵为 $C_x$,那么白化变换就需要得到一个变换矩阵 $W$,使得
为白化向量。我们知道 $X$ 的自协方差矩阵的表达式为:
那么 $Y$ 的协方差矩阵为 $\Sigma=WC_x W^{T}$。(这个直接把 $Y$ 与 $X$ 的关系代入上式就可以得到),所以要使得 $WC_x W^{T}=E$。白化变换的关键就是求出满足上述条件的变换矩阵 $W$,求解方法不唯一。设 $C_x=U\Lambda U^T$ 为 $C_x$ 的特征值分解,其中 $U$ 是正交矩阵(正交阵是指满足 $AA^T=E$ 或者 $A^TA=E$ 的 $n$ 阶方阵 $A$),那么 $W=R\Lambda^{-1/2}U^T$ 都是满足条件的白化变换矩阵,其中 $R$ 为任意正交矩阵。特别地,我们称
为PCA变换,称
为ZCA变换或马氏变换。
参考文献
白化(Whitening) | Jacky’s blogs (wangjs-jacky.github.io)
Whiten process——数据的白化处理-CSDN博客
二维均匀分布:rand
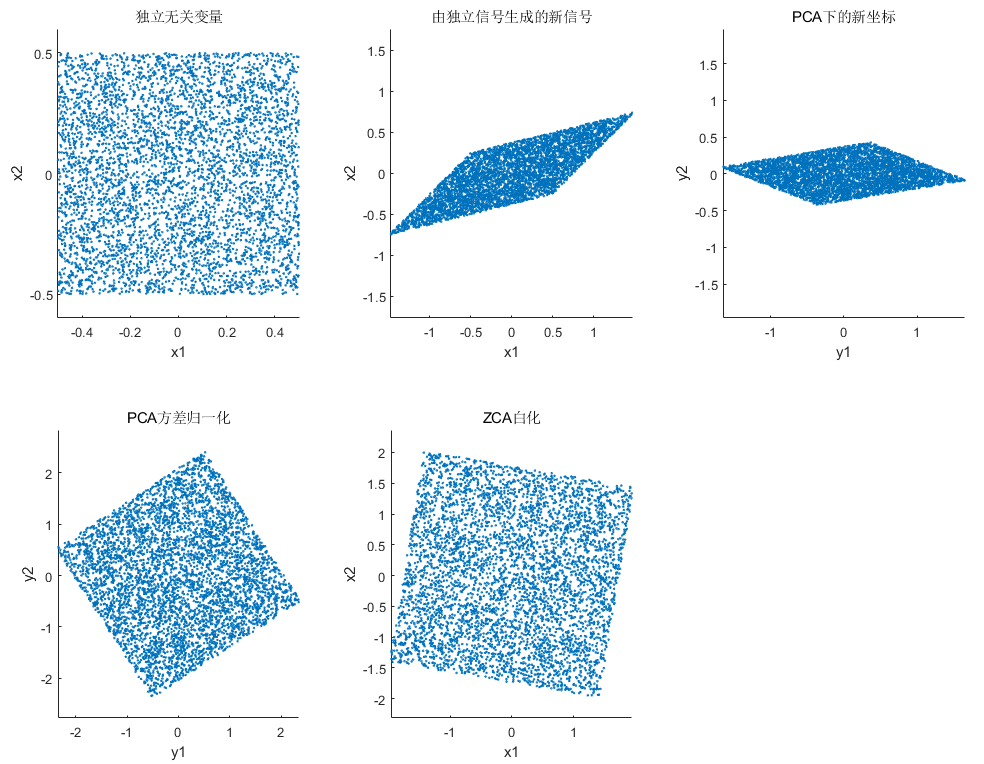 二维高维分二维高斯分布:
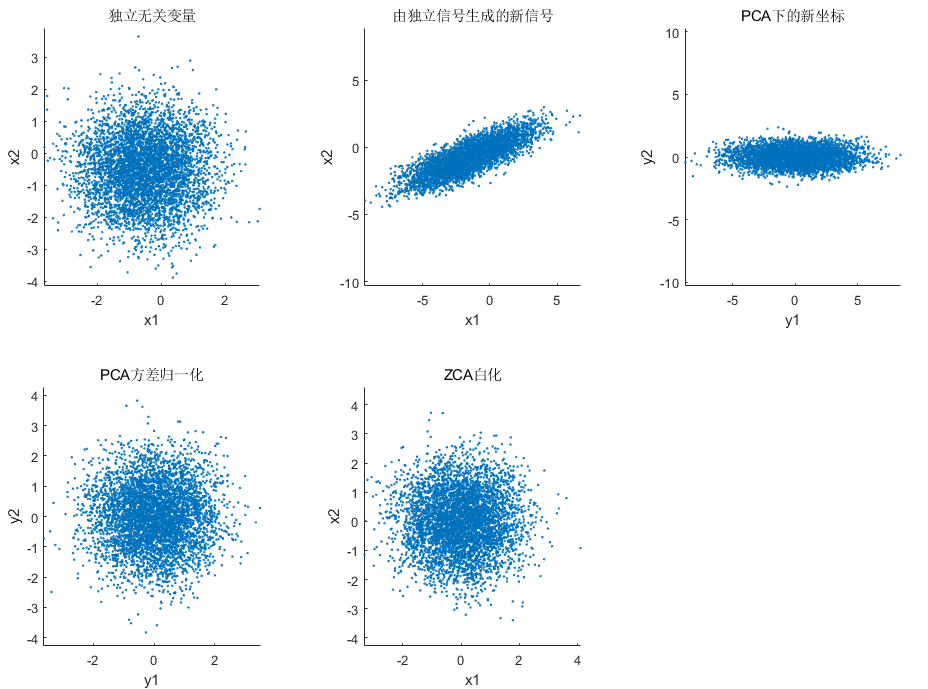
二维高维分二维高斯分布:randn
注:这里的 PCA白化和 ZCA白化看上去一样其实是不一样的,PCA的数据在维度方向是无关的,相当于原数据发生了一个旋转,ZCA则与原数据没有发生旋转,从第一个图可以发现这种旋转方式。下图可以反映这种变换。