参考知乎讲解:小白爱上SPSS - 知乎 (zhihu.com)
参考b站视频:单因素方差分析(上)/ANOVA/什么是方差分析、方差分析的思路_哔哩哔哩_bilibili
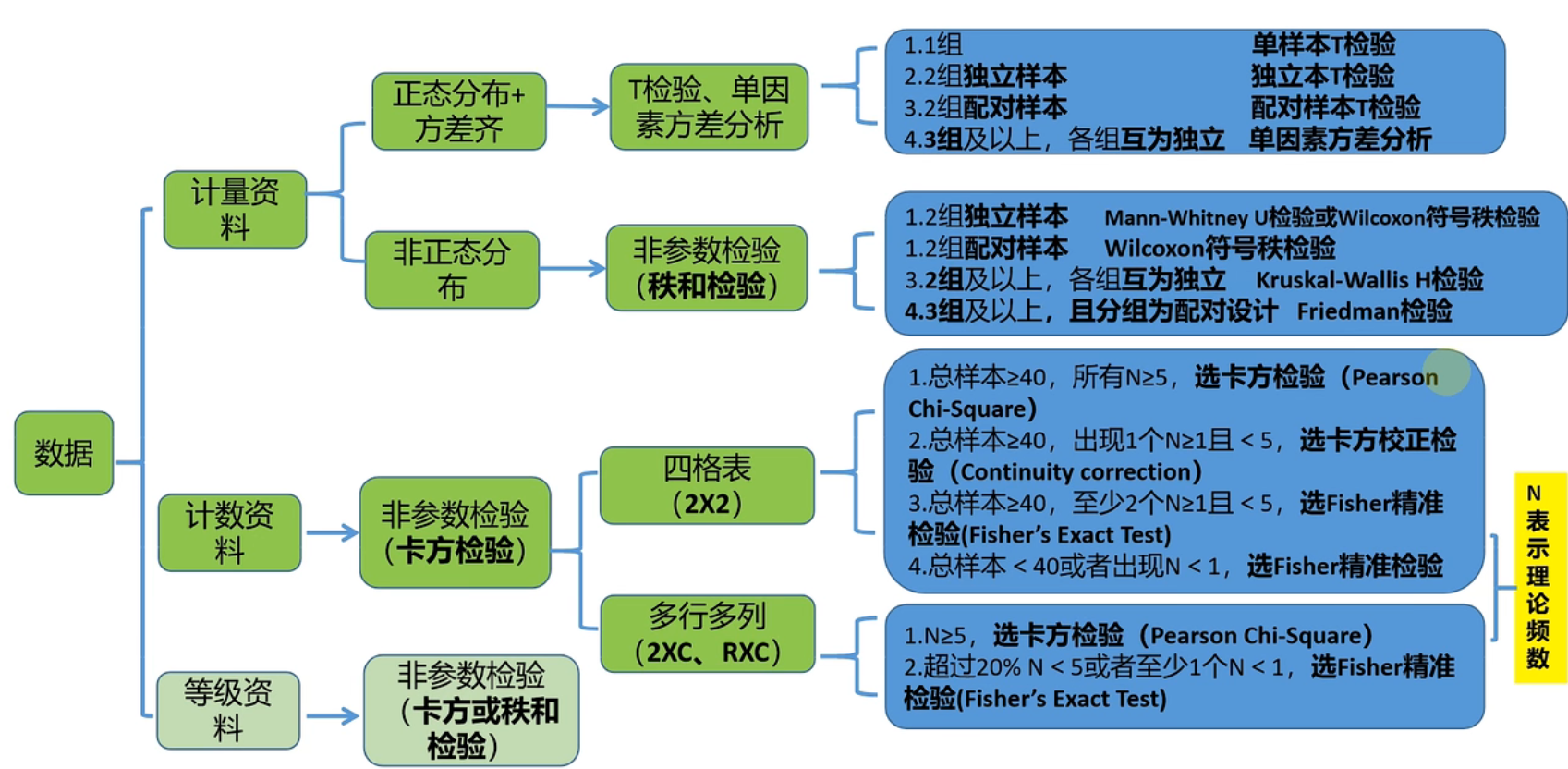
什么时候用什么检验:
正态分布:
计数资料:
单个计数资料:单样本比例检验
多个计数资料:卡方检验
计量资料:
- 两组数据:t检验(可以和计数资料结合)
- 多组数据:ANOVA(可以和计数资料结合)
非正态分布:
- 秩和检验
几个重要参数:
- \(\alpha\):显著性水平,是 \(p\) 值的临界值,一般比较小,如:0.01,0.05.
- \(p\):表示在 H0成立的情况下,拒绝 H0,接受 H1的错误决策的概率。可以理解为风险,\(p\) 值越小,拒绝 \(H_0\) 的风险越低。这个参数的值需要与显著性水平比较,若小于显著性水平,则拒绝假设 \(H_0\),并称观察到的差异在统计上是显著的
1. 方差分析
- 单因素方差分析
- 双因素方差分析
1.1 单因素方差分析
1.1.1 方差分析的基本概念
目的: 比较不同分组 (通常组别大于等于3) 之间某一特征值的均值是否存在显著差异。(n个分类,它们的某一特征值的平均值,是否有显著区别)
因素 (factor or independent variable) : 一定是分类型变量,且类别大于3。例子:
- 视频分区:生活区、知识区、游戏区、美妆区、搞笑区
- 医学院:协和、北医、复旦医学院、上交医学院、Harvard medical school.John's Hopkins medical school、 UCSF medical school
特征值 (dependent variable): 一定是连续型变量
原假设: \[ H_{0}\colon\mu_{1}=\mu_{2}=\mu_{3}=\cdots=\mu_{n} \]
备择假设: \[ H_1{:}\mu_1{:}\mu_2{、}\mu_3{、}...{\mu_n} 不全相等 \]
1.1.2 方差分析的思路
数据整体波动(Sum of Squares Total):组内波动与组间波动。整体波动描述的是所有数据,包含了各个分组数据。
组内波动(Sum of Squares Within, SSW):
- 某一分组内,个体特征值的离散程度
- 例子:协和医学院学生考试成绩的离散程度
组间波动(Sum of Squares Between, SSB):
- 不同分组之间,分组特征值的平均值的离散程度
- 例子:协和医学院、北大医学院、哈佛医学,学生考试成绩均值的离散程度
\[ SST = SSB + SSW \]
一些结论和例子:
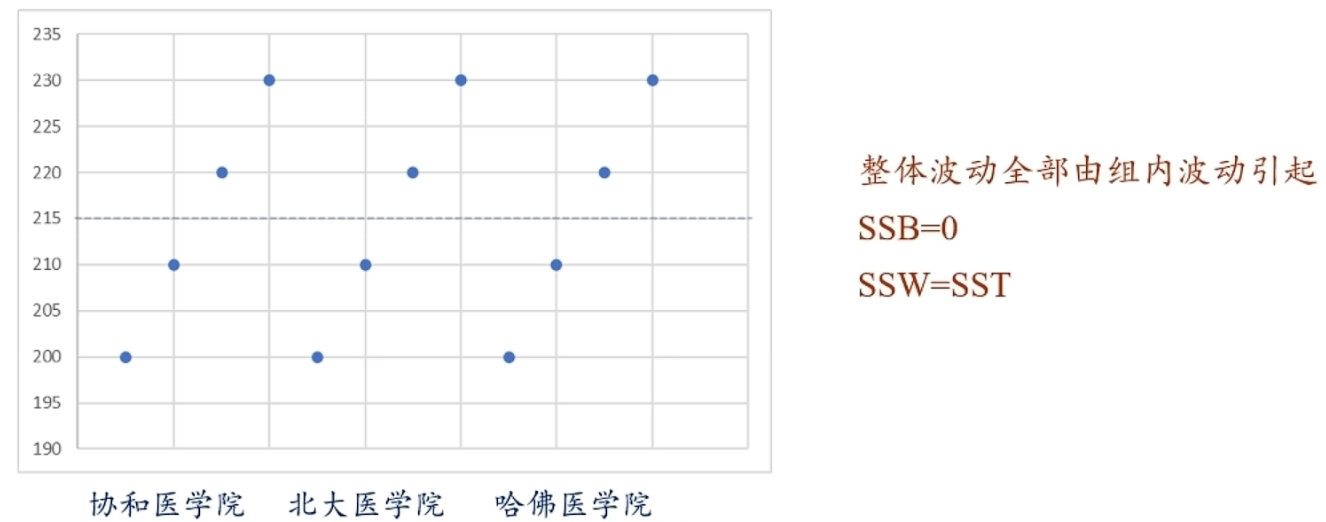
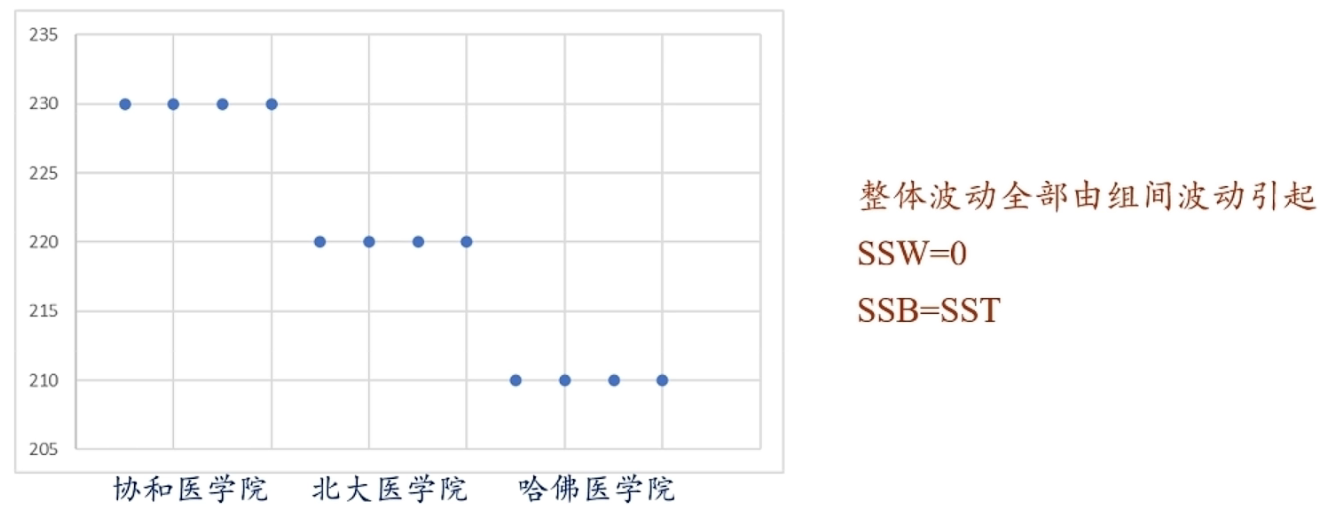
- 组内波动占整体波动越大,组间波动占整体波动越小,各组均值相等的可能性越大
- 组内波动占整体波动越大,组间波动占整体波动越小,各组均值相等的可能性越大
我们通过构造 f 统计量来判断我们的组间波动,它的占比是否足够的大,大到让我们拒绝原假设
1.1.3 怎么计算SST SSW SSB,利用F检验进行判断
计算SST: \[
\text{Sum of Squares Total=}\sum(x_i-\bar{\bar{x}})^2
\] 
计算SSW: \[
\text{Sum of Squares Within}=\sum(x_i-\overline{x_i})^2
\] 
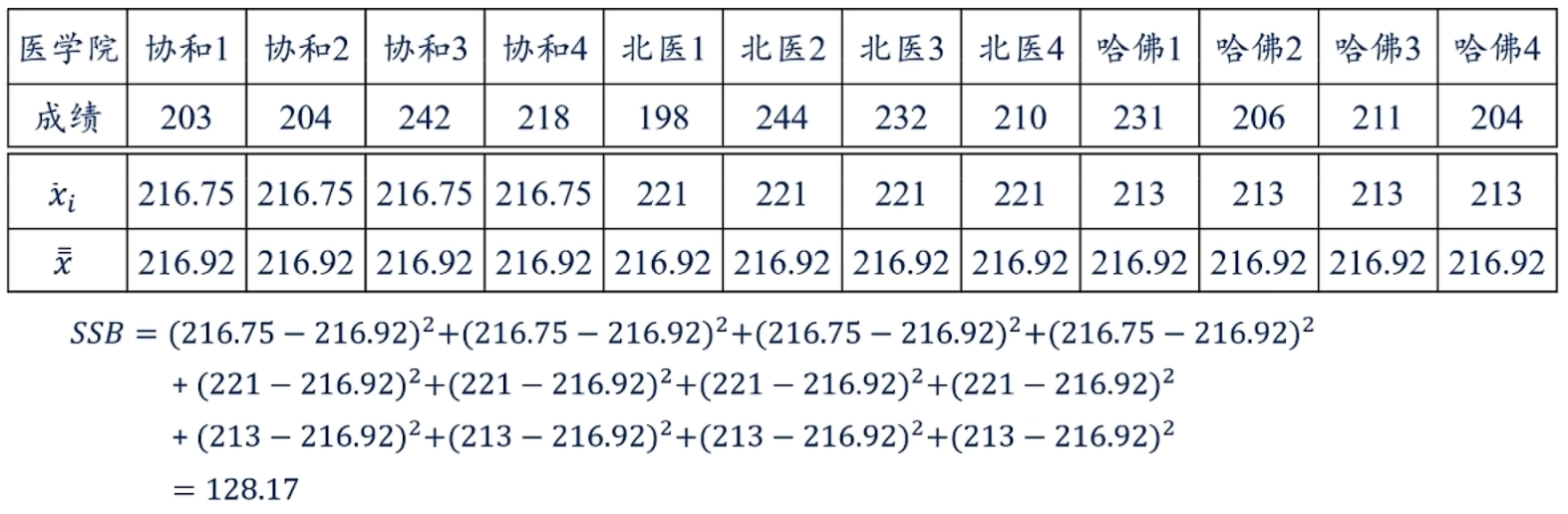
计算SSB: \[
\text{Sum of Squares Between}=\sum(\overline{x_i}-\bar{\bar{x}})^2
\] 
构造F统计量(符合F分布):

组间自由度:组别数量-1
组内自由度:Σ(每组个体数量 - 1)
通过查表格确定F统计量所对应的p值是多少

1.2 双因素方差分析
特征值同时受两个因素影响。e.g. 视频播放量同时受 视频分区 和 up主学历 影响。双因素方差分析因素的组别不做限制,不需要像单因素方差分析那样必须大于三组。双因素方差分析探讨的三个问题:
问题一:根据第一个因素进行分组时,不同分组之间的特征值均值是否相等
- 原假设:第一个因素对特征值均值没有显著影响
- 备择假设:第一个因素对特征值均值存在显著影响
问题二:根据第二个因素进行分组时,不同分组之间的特征值均值是否相等
- 原假设:第二个因素对特征值均值没有显著影响
- 备择假设:第二个因素对特征值均值存在显著影响
问题三:第一个因素和第二个因素的交互效应,是否对不同分组之间的特征值均值产生影响
原假设:交互效应对特征值均值没有显著影响
备择假设:交互效应对特征值均值存在显著影响
1.2.1 双因素方差分析思路
计算五个波动:
- 数据整体波动(sum of squares total)
- 第一个因素所带来的波动(sum of squares first factor)
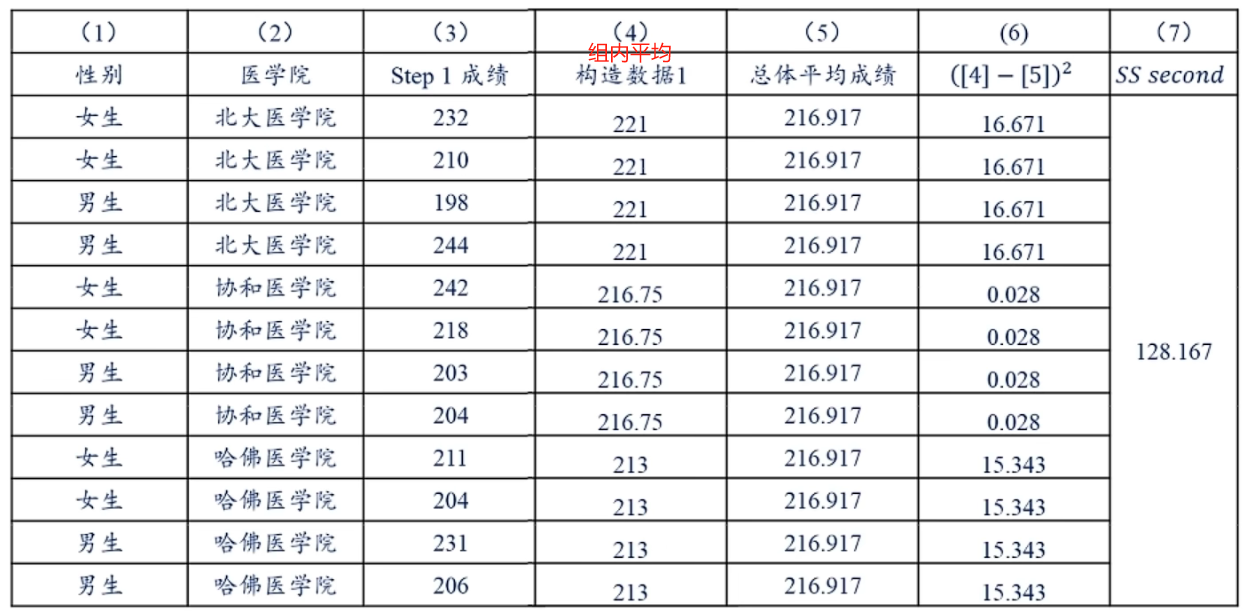
- 第二个因素所带来的波动(sum of squares second factor)
- 两个因素交互项所带来的波动(sum of squares interaction)
- 误差项所带来的波动(sum of square error)
五个波动之间的关系: \[ SST = SSFF + SSSF + SSI + SSE \] 模型所带来的波动(sum of square model): \[ SSM = SSFF + SSSF +SSI \] 为什么叫模型带来的波动呢?因为双因素方差分析可以理解为两个因素构成了这样一个检验模型,用这个模型来解释特征值的波动,前三项波动就是这个模型能够解释的部分。误差项时这个模型不能解释的部分。下面分情景进行解释:
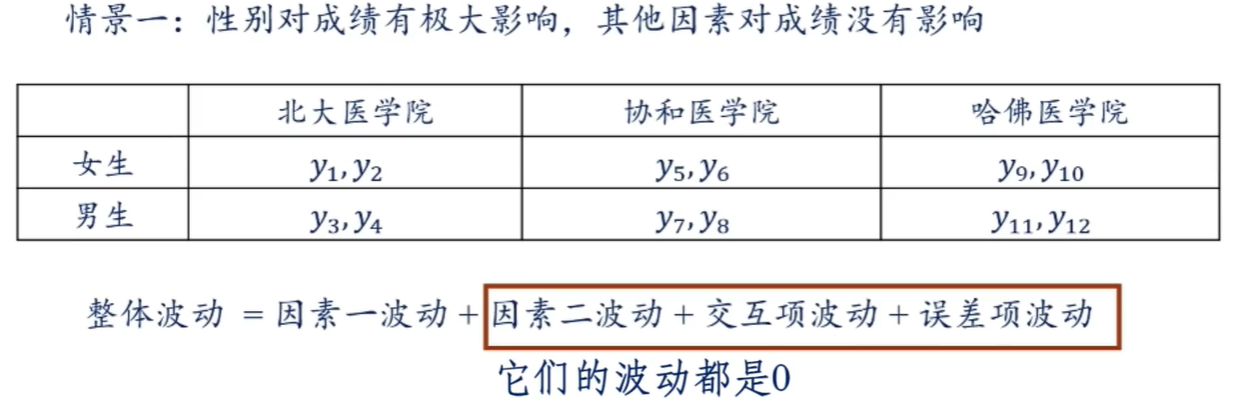
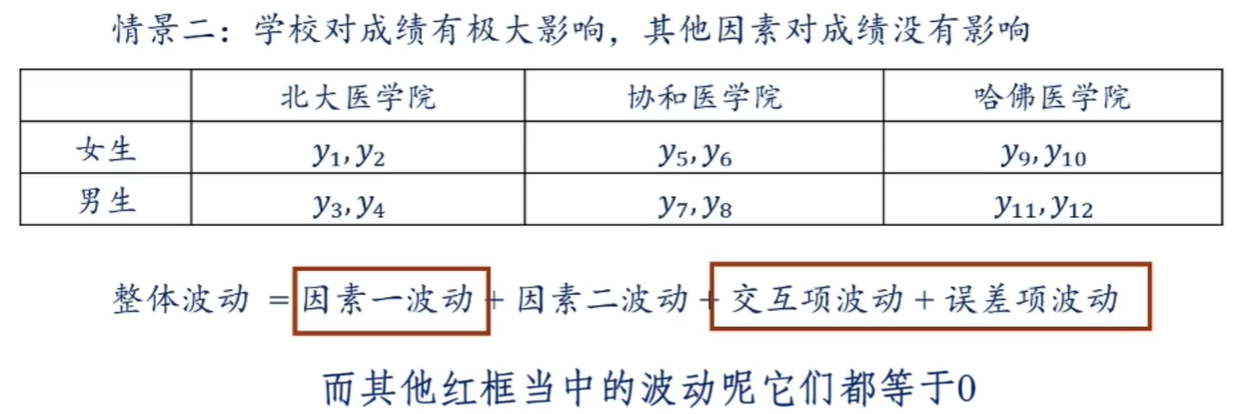
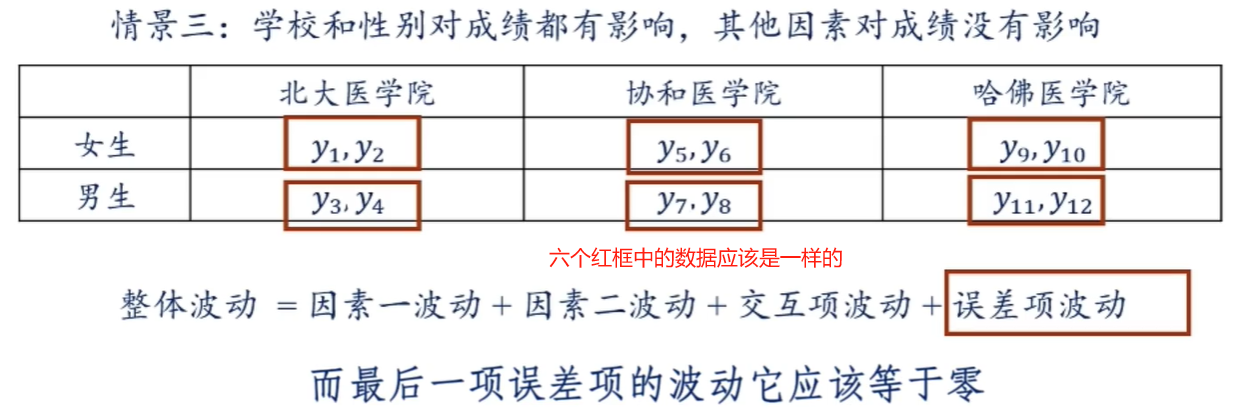

1.2.2 双因素方差分析思路
- 计算出因素一波动 、因素二波动 、交互项波动 、误差项波动
- 分别将因素一波动 、因素二波动 、交互项波动,与误差项波动进行比较
- 因素一波动 v.s 误差项波动进行比较(如果因素一波动显著大于误差项波动,那么就说因素一对特征值有影响)
- 因素二波动 v.s 误差项波动进行比较(如果因素二波动显著大于误差项波动,那么就说因素二对特征值有影响)
- 交互项波动 v.s 误差项波动进行比较(如果交互项波动显著大于误差项波动,那么就说交互项对特征值有影响)
1.2.3 波动的计算方法
- SST:每个个体的数值减去总体的平均值的平方和
- SSFF:构造一组数据,使得这组数据只受因素一影响
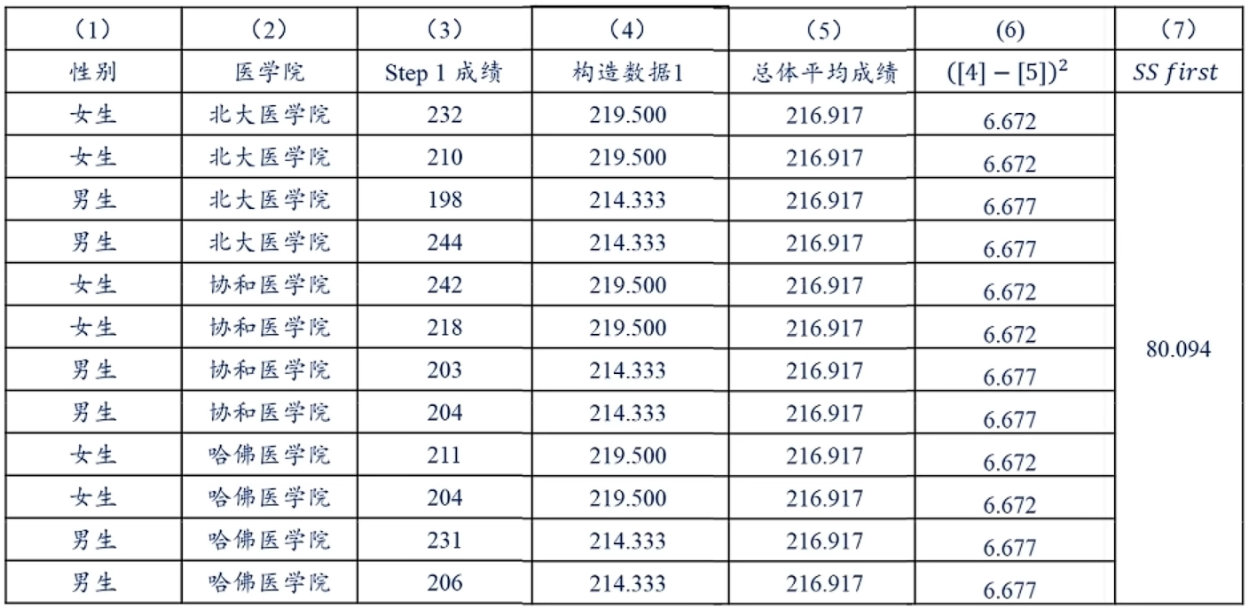
- SSSF:构造一组数据,使得这组数据只受因素二影响
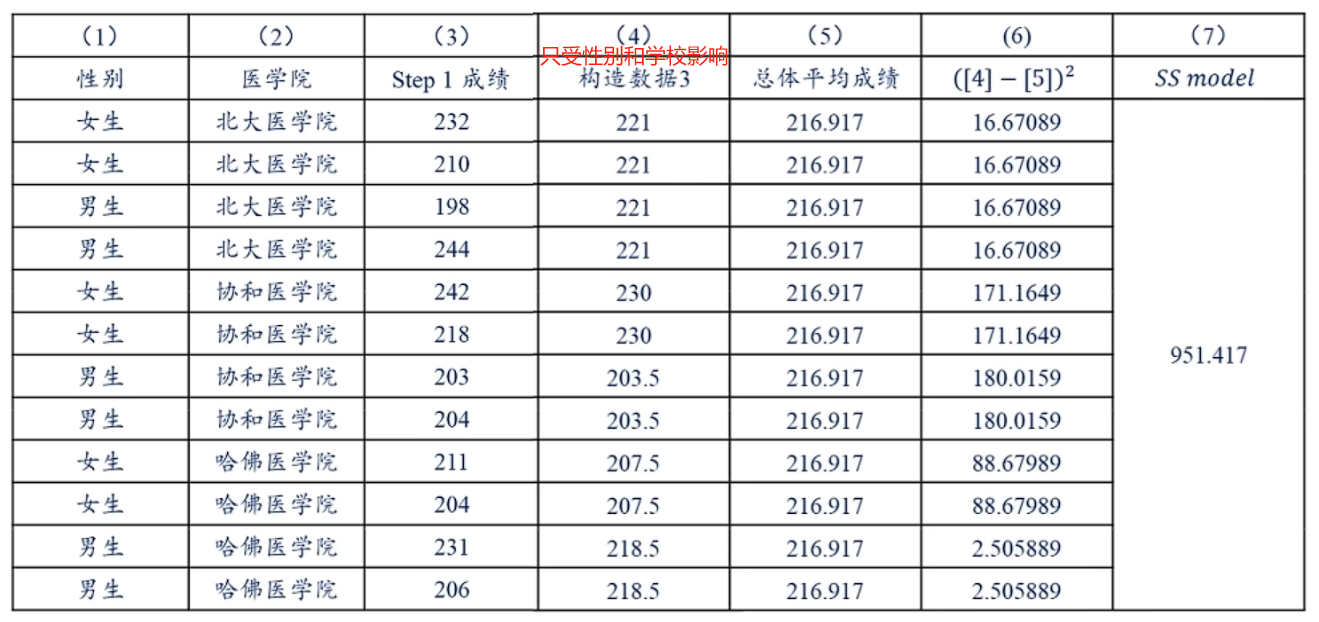
- SSM:构造一组数据,使得特征值受两个因素影响
- SSI:SSM - SSFF - SSSF
- SSE:个体取值 - 模型所能解释的取值(SST - SSM)
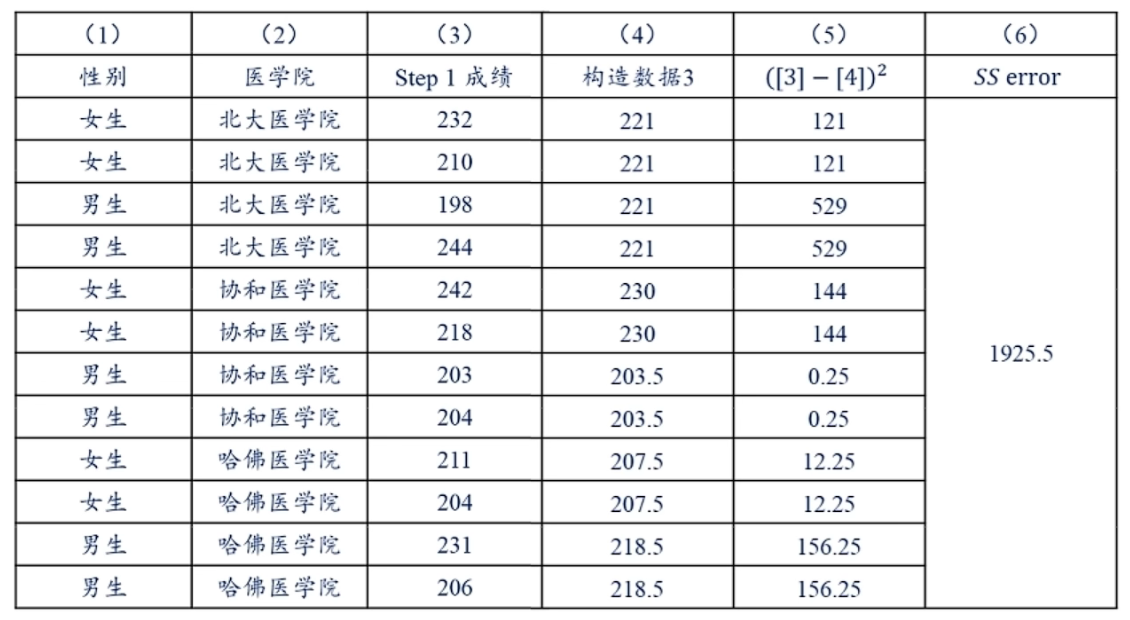
构造F统计量(符合F分布):
- sum of squares first 自由度:因素一分组数减1 = 2 -1 = 1
- sum of squares second 自由度:因素二分组数减1 = 3 -1 = 2
- sum of squares interaction 自由度:模型自由度减去因素一自由度减去因素二自由度 = (2 x 3 -1) - 1- 2 = 2
- sum of squares error 自由度:整体自由度减去模型自由度 = (12 - 1) - (2 x 3 -1) = 6
