生物信号、语音信号、雷达信号等随机信号具有易变性,因此通常使用属性而不是波形自身来度量,因为属性对变化的敏感度较低。
参考书籍:《Fundamentals of statistical signal processing: Estimation theory》
Chapter 1 无偏估计
无偏估计值估计量的期望等于真实值:
与无偏估计相对应的是有偏估计,无偏估计并不一定是好的估计,只代表估计量的期望等于真值。
Chapter 12 线性贝叶斯估计量
保留MMSE准则,但是限定估计量是线性的。
线性估计量的形式:
选择加权系数 $a_n$ 来使贝叶斯 MSE 最小。贝叶斯 MSE:
导出的估计量称为线性最小均方误差(LMMSE)估计量.
一个例子帮助理解:
考虑一个参数θ,它根据单一数据 $x[0]$ 来估计, 其中 $x[0] \sim \mathcal{N}\left(0, \sigma^2\right)$ 。如果待估计的参数是 $x[0]$ 现实的功率, 即 $\theta=x^2[0]$,那么理想的估计量是:
因为最小贝叶斯 MSE 将等于零。很显然这个估计量是非线性的。然而, 如果我们试图应用 LMMSE 估计量, 即:
那么最佳加权系数 $a_0$ 和 $a_1$ 可以通过使:
最小而求出。
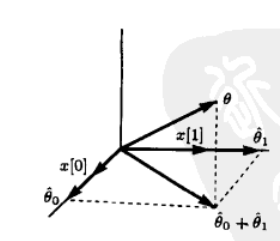
几何意义:
矢量长度的定义:对于一个零均值的变量来说,它的长度定义为方差的平方根($|x|=\sqrt{E\left(x^2\right)}$),方差越大矢量长度越长。
如果两个矢量是正交的,那么我们不能用其中的一个来估计另一个参数,因为在x方向没有y的分量,所以我们可以只考虑投影带来的关系。
LMMSE 估计量:$\hat{\theta}=\sum_{n=0}^{N-1} a_n x[n]$
优化目标:$E\left[(\theta-\hat{\theta})^2\right]=E\left[\left(\theta-\sum_{n=0}^{N-1} a_n x[n]\right)^2\right]=\left|\theta-\sum_{n=0}^{N-1} a_n x[n]\right|^2$
$\theta$ 与估计量 $\hat{\theta}$ 之差的期望与所有 $x[n]$ 张成的向量垂直,最终估计量 $\hat{\theta}$ 是 $\theta$ 在 $x[n]$ 张成的轴上的投影的和。e.g. $\hat{\theta}=\hat{\theta}_0+\hat{\theta}_1$