Multichannel Blind Source Separation Using Convolution Kernel Compensation

DEMUSE Tool是提出这个算法的学者开发的matlab工具箱，但是不开源，其官网链接为：DEMUSE Tool (um.si)。这个网站中对sEMG的产生机理、CKC算法做了非常详细的描述，十分值得一看。Holobar主页：https://so3.cljtscd.com/

---

2023/12/11

• 为什么叫卷积核补偿算法？

  因为表面肌电信号是一个卷积混合模型，而矩阵H就是卷积核，通过计算马氏距离的平方，CKC算法对这个卷积核进行了补偿，直接估计了MUST。

• 对该算法的理解

  该算法通过线性最小均方误差估计器对脉冲序列进行估计：

  $$\hat{t}_j(n)=\mathbf{c}_{t_j\mathbf{x}}^T\mathbf{C}_{\mathbf{x}\mathbf{x}}^{-\mathbf{1}}\mathbf{x}(n)=\mathbf{c}_{t_j\bar{\mathbf{t}}}\mathbf{H}^T\left(\mathbf{HC}_{\overline{\mathbf{t}}\overline{\mathbf{t}}}\mathbf{H}^T+\mathbf{C}_{\omega\omega}\right)^{-1}\mathbf{H}\bar{\mathbf{t}}(n)$$

  但是 $\mathbf{c}_{t_j\bar{\mathbf{t}}}^T$ 事先不知道，因此首先需要赋一个初值。不失一般性，假设第 j 个 MU 在 n1时刻发放，那么设 $\hat{\mathbf{c}}_{t_j\mathbf{x}}=\mathbf{x}(n_1)$，那么得到发放序列的第一个估计：

  $$\hat{t}_j(n)=\mathbf{\hat{c}}_{t_j\mathbf{x}}^T\mathbf{C}_{\mathbf{x}\mathbf{x}}^{-1}\mathbf{x}(n)$$

  选取 $\hat{t}_j(n)$ 中最大峰值的时刻作为可能的第二次发放的时刻，并更新 $\hat{\mathbf{c}}_{t_j\mathbf{x}}$：

  $$\mathbf{\hat{c}}_{t_j\mathbf{x}}=\frac{\mathbf{\hat{c}}_{t_j\mathbf{x}}+\mathbf{x}(n_2)}2$$

  然后按照上述过程不断循环。有一个问题是，如何初始化这个n1呢？（已通过激活指数解决）

2023/12/26

• 对该算法的理解：

  我们知道，分离向量是找到一个时刻，然后相关矩阵的逆矩阵乘以该时刻的观测值列向量就得到了分离向量。文章说先是计算激活指数，然后如果第j个MU在n0时刻发放的话，那么 $s_{n0}(n)=\bar{X}^T(n_0)C_{\overline{X}\overline{X}}^{-1}\bar{X}(n)$ 就是第 j 个MU的IPT估计，后续只需要通过下述表达式改进这个观测值列向量就行：

  $$C_{\bar{X}_{sj}}=\frac1{\operatorname{card}(\varphi_n)}\sum\bar{X}(\varphi_n)$$

_2023/12/29_

• 为什么有这么一个取平均的操作？

  注意到 CKC 算法的关键是估计相关向量 $\mathbf{c}_{t_j\mathbf{x}}$，但是由于 $t_j$ 事先是不知道，因此无法直接计算。而 $\mathbf{c}_{t_j\mathbf{x}}=E(t_j(n)\mathbf{x}(n))$ 这个计算公式表明，$\mathbf{c}_{t_j\mathbf{x}}$ 是第 $j$ 个 MU 发放时刻 $t$ 的发放时刻处，观测向量的期望，而期望就是取平均，所有才有了取平均估计相关向量这么一个操作。

_2024/1/2_

• 对相关矩阵进行截取操作

  这个操作是为了减小噪声带来的干扰，在SNR=15dB时，截取程度为0%，在SNR为0dB时，截取程度为20%。

_2024/1/10_

• n0时刻的相关向量分离得到的spike train，只有那些在n0时刻发放的mu对这个spike train有贡献，也就是说，使用n0时刻的观测向量作为相关向量，只要是在n0时刻发放的mu，它们的脉冲都会被加强，只是其他时刻的脉冲幅值加强程度没有n0时刻强。而其他没有在n0时刻发放的mu则在幅值上贡献的非常少。所以一般情况下某个时刻只有一个脉冲序列发放，因此该时刻的分离向量分离得到的spike，幅值较高的都来自于这个脉冲序列。

• 两个互补假设：从vn0和vn1做内积得到的spike train中选取脉冲时刻nr，这个nr对应的脉冲序列有两种情况（1）如果Gn0∩Gn1不为空，那么做内积之后的集合代表了同时在n0和n1发放的mu，因此这个mu的脉冲被加强，所以nr也是这个mu的脉冲，所以至少有一个mu在n0和n1和nr发放；（2）如果Gn0∩Gn1为空，那么至少存在两个脉冲，都在nr处发放，其中一个在n0和nr处发放，另一个在n1和nr处发放。

• 取哪个时刻的观测向量作为相关向量，那么该时刻的脉冲就被加强，对应mu的其他脉冲也加强，只是幅值稍低。所以分解算法的收敛条件是对所有发放时刻的观测向量取期望作为相关向量，使用这样一个平均的相关向量进行分离得到的spikes在幅值上都是接近的。所以这就是最终的收敛条件。

  

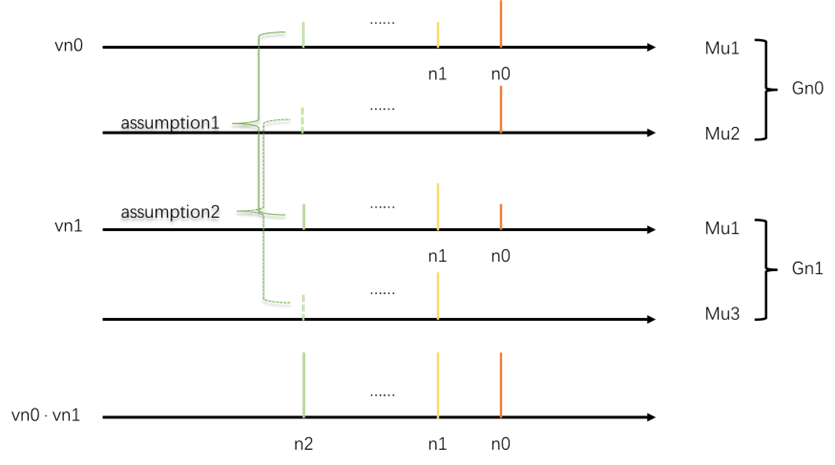
• CKC算法一般取4个发放时刻，通过两个假设以及这几个时刻的spike数目来对这些spike的归属进行判断，如果都是来自于同一个MU，那么通过对这些发放时刻的观测向量取均值，得到相关向量，然后得到spike。

2024/3/6

• 对相关矩阵 $C$ 的理解，假设有这么一个信号： $$\begin{gathered}\mathbf{y}=\begin{bmatrix}a1&a2&a3&...\\b1&b2&b3&...\end{bmatrix}\\C_\mathbf{y}=E[\mathbf{y}(n)\mathbf{y}(n)^T]=\frac13(\begin{bmatrix}a1a1&a1b1\\a1b1&b1b1\end{bmatrix}+\begin{bmatrix}a2a2&a2b2\\a2b2&b2b2\end{bmatrix}+\begin{bmatrix}a3a3&a3b3\\a3b3&b3b3\end{bmatrix}+...)\end{gathered}$$ 可以看到如果两个通道中没有 MUAP 重合，那么交叉项就很小，矩阵对角占优。

1. 笔记

$$x_i(n)=\sum_{j=1}^N \sum_{l=0}^{L-1} a_{i j}(l) t_j(n-l) ; \quad i=1, \ldots, M$$

symbol 的长度为 L，也就是 $a_{ij}$ 的长度是 L。如果不考虑 N 个源的叠加，那么就是 $a_{ij}(n)$ 与 $t(n)$ 的卷积，该表达式的意义就是对于某一个观察或检测，其值等于一个源的发放时间与观测位置处 symbol 的卷积，再对所有源求和的一个结果。

超定和欠定主要是看混合矩阵A的行KM与列N(L+K-1)的大小，KM大则是超定，KM小则是欠定。

采样率高了之后，两个峰值之间的采样点就多了，因此就相当于变得稀疏了。

Moreover, when sampling frequency is high enough (with respect to the symbol rate), the pulse trains become highly sparse.

$$\overline{\mathbf{y}}(n)=\mathbf{A} \overline{\mathbf{t}}(n)+\overline{\boldsymbol{\omega}}(n)$$

混合矩阵A中包含的信息实际上是被忽略了的，CKC算法更关注脉冲序列的性质。

CKC 算法用于求取脉冲序列，也就是上式中的 $\overline{\mathbf{t}}(n)$，求得的结果是对 $\overline{\mathbf{t}}(n)$ 的最佳线性贝叶斯估计，线性贝叶斯估计是求取一组最佳的权重，将信号每一个时间点的值加权求和来估计参数。

1.0 符号说明

• 时间扩展向量（在 n 这个时刻对 N 个源信号扩展）， 维度：1 × N (K+L-1)：

  $$\begin{array}{r} \overline{\mathbf{t}}(n)=\left[t_1(n), t_1(n-1), \ldots, t_1(n-L-K+2), \ldots,\right. \left.t_N(n), \ldots, t_N(n-L-K+2)\right]^T \end{array}$$

  时间扩展向量中的第j个元素（这个元素可能是n时刻的，也可能是n时刻前的）：$\bar{t}_j(n)$

• 把 $\overline{\mathbf{t}}(n)$ 中的第 j 个元素在每个 n 时刻都取出来构成向量：$\overline{\mathbf{t}}_j=\left\{\bar{t}_j(n) ; n=0,1, \ldots\right\}$

• 全局活跃指数：$\gamma=\{\gamma(n) ; n=0,1, \ldots\}$ ，$n_k$ 时刻不为0，则至少存在一个j，使得 $\overline{\mathbf{t}}(n_k)$ 中的第j个元素 = 1。即： $\gamma\left(n_k\right)>0 \Leftrightarrow \exists j;\bar{t}_j(n) =1$。

• 当 $n_0$ 时刻存在 $g_0$ 个 j 时，j 的一个集合：

  $$G_{n_0}=\left\{j_{n_0, 1}, \ldots, j_{n_0, g_0}\right\} \text {, i.e., } j \in G_{n_0} \Leftrightarrow \bar{t}_j\left(n_0\right)=1$$

  观测扩展向量：

  $$\begin{aligned}\overline{\mathbf{y}}(n)=[y_1(n),y_1(n-1),\ldots,y_1(n-K+1),\ldots,y_M(n),\ldots,y_M(n-K+1)]^T\end{aligned}$$

1.1 超定情况

symbols的个数N少于观测的个数M（源的个数少于通道的个数），脉冲序列相关性很弱（比如有少量但确实存在的脉冲重叠）。此外，假设观测值是遍历的，并用扩展观测值的相关矩阵表示。最后，假设扩展因子足够大，且矩阵是满列秩的。

激活指数（怎么得到的这个表达式？）：

$$\begin{aligned} \gamma(n) & =\overline{\mathbf{x}}^T(n) \mathbf{C}_{\overline{\mathbf{xx}}}^{-1} \overline{\mathbf{x}}(n) \\ & =\overline{\mathbf{t}}^T(n) \mathbf{A}^T\left(\mathbf{A}^T\right)^{-1} \mathbf{C}_{\overline{\mathbf{tt}}} \mathbf{A}^{-1} \mathbf{A} \overline{\mathbf{t}}(n) \\ & =\overline{\mathbf{t}}^T(n) \mathbf{C}_{\overline{\mathbf{t t}}}^{-1} \overline{\mathbf{t}}(n) \end{aligned}$$

激活数的发放时间表示形式只需要把公式 $\overline{\mathbf{x}}(n)=\mathbf{A} \overline{\mathbf{t}}(n)+\overline{\boldsymbol{\omega}}(n)$ 忽略噪声代入即可。激活指数是全局脉冲序列活动的一个指标，在某个时刻时，只有当至少有一个脉冲序列在此刻发放，那么激活指数才不为0，因为C中的元素是时刻之间的自相关系数和互相关系数，均不为0（其逆也不为0），所以只要存在一个MU的发放脉冲，那么相乘相加后一定是大于0的。

当我们用存在发放时刻的观测序列去代替原观测序列后，有如下表达式：

$$\begin{aligned} \nu_{n_0}(n) & =\overline{\mathbf{x}}^T\left(n_0\right) \mathbf{C}_{\overline{\mathbf{x x}}}^{-1} \overline{\mathbf{x}}(n)=\overline{\mathbf{t}}^T\left(n_0\right) \mathbf{C}_{\overline{\mathbf{t t}}}^{-1} \overline{\mathbf{t}}(n) \\ & =\sum_{k \in G_{n_0}} \sum_{j=1}^{N(L+K-1)} c_{j k}^{\mathrm{inv}} \bar{t}_j(n) \end{aligned}$$

注意，这个表达式中的j代表的是时间扩展向量中的第j个元素，在左边项取了n0后，t的值就变成了1或者0，0项在求和过程中可以忽略，1作为系数时也省略不写，因此可以化简成上式求和的形式。上式中j代表的是行，k代表的是列，可以看到行是全部索引完的，而列只取矩阵中激活的列，即t中每一个元素与C中的列对应相乘，最后再求和。

附录A证明，C拥有优越的对角线，是对角占优的，所有可以忽略掉非对角线的部分，得到如下公式：

$$\nu_{n_0}(n) \approx \sum_{j \in G_{n_0}} c_{j j}^{\operatorname{inv}} \bar{t}_j(n) .$$

注意，上述公式中，n 是遍历所有采样点的，只有当 n=n0 时，$\nu_{n_0}$ 才不等于0（因为j是在 n0 时取的，一旦错位最终结果就是0），这样也就在时间轴上找到了n0。但是也存在一些偶然情况，比如考虑n0时刻，其脉冲集合是 $G_{n_0}$，而当 n 遍历到 n2 时，这时如果 n2 时间序列的第 $j_{n_0,1}$ 个元素恰好与n0时间序列的 $j_{n_0,2}$ 重合，那么该式得到的结果也不是0，这样就会找到两个时刻点 n0 和 n2 ，因此，还需要对这些时刻进行分离，示意图如下：

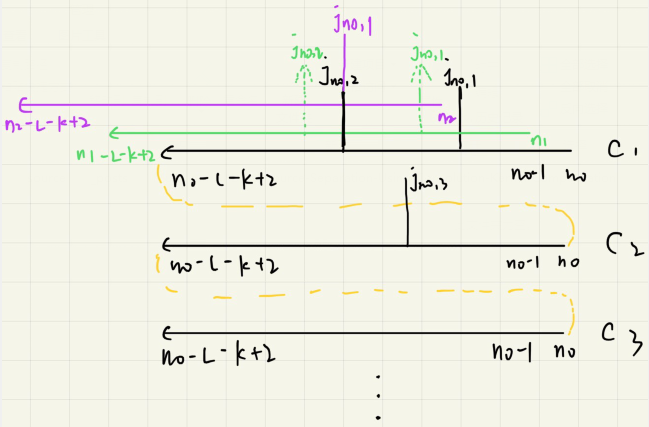
1.2 脉冲序列的分离

从上图可以看到，$G_{n_0}$ 和 $G_{n_2}$ 中至少存在一个脉冲重叠。对 $\nu_{n_0}$ 和 $\nu_{n_2}$ 做内积（$\nu_{n_0}(n) \cdot \nu_{n_1}(n) ;$ $n=0,1,2, \ldots$），得到一个序列，记为 $\mathbf{h}_{n_0, n_1}$，再随机选择 R-2个脉冲记为 $n_r ; r=2, \ldots, R-1$。对于 $n_r$，有两个互补（两者之一必成立）结论：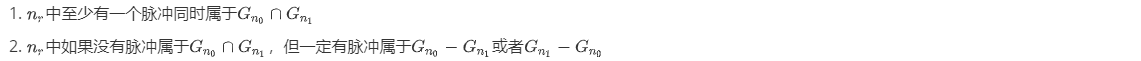

对每一个 $n_r ; r=2, \ldots, R-1$，求 $\mathbf{v}_{n_r}$，并生成集合 $G_{n_r}=\left\{j_{n_r, 1}, \ldots, j_{n_r, g_r}\right\}$。再对所有的 $\nu_{n_r}(n)$ 求内积得到最终序列。