重要程度: ⭐⭐⭐⭐⭐
阅读这篇文献是因为阅读的 Non-Invasive Analysis of Motor Unit Activation During Simultaneous and Continuous Wrist Movements 这篇文献在介绍其分解流程时引用了这篇文献,想通过该文献来详细了解分解流程。这篇文章介绍了如何实时分解高密度肌电得到运动单元。方法也比较简单,就是先训练得到 MUST 的分离矩阵和相关参数,然后对在线采集的高密度肌电直接使用训练得到的分离矩阵和相关参数从而得到 MUST。文章从仿真数据和真实数据两个方面进行了验证,重点关注了一下实验范式。
这篇文章还研究动态下的分解效果,通过数据手套来记录关节数据,重点参考。提出的更新算法也主要是对动态的数据有用。之前有文章研究了实时的分解,但是局限在静态的条件下,也有文章研究了动态的分解,但是是离线的,这篇文章同时实现了实时的MUST识别,还能够适用于非静态的条件。
本文的思路是这样的,要研究实时的分解效果,也就是研究在一个滑动窗中间的分解效果:首先通过前10s分解得到分离参数,然后对剩余的信号采用滑动窗口,在这个窗口中,采用了更新策略分解出的 MU 更多,而直接使用静态 gckc 算法得到的 MU 更少。思路很重要:等式 (1) 中的混合矩阵 H 在等长收缩中是恒定的,但在非等长条件下随时间变化,这需要相应的分离向量进行更新。
1.笔记
1.1 引言
a decomposition method robust to changes of motor unit action potential (MUAP) has been proposed and can be used for the identification of motor unit firings during dynamic contractions.
什么是静态?静态就是兴奋的水平(频率)和MUAP的波形不变。
对于兴奋程度改变,MUAP改变的情况,不能直接把离线的分离向量用在在线的分解上,因此需要对分离向量等参数进行更新。但是之前使用的CNN是可以的。
1.2 分解流程
Two sessions:
- offline session:得到估计参数、分离MUST的矩阵、以及spike提取的阈值
- online session:滑动窗口中,将预处理过后的EMG信号与分离矩阵直接相乘,得到发放序列
在离线步骤中,首先使用卷积核补偿(CKC)算法将表面肌电信号分解为MUST。
多通道表面EMG信号的生成模型可以描述为一系列脉冲的卷积混合,代表运动单元的放电模式(diacharge pattern)。该混合模型中滤波器的脉冲响应是运动单元的动作电位,其持续时间有限。混合过程可以矩阵形式写成:
\[ y(n)=H \bar{s}+\omega(n) \] CKC方法补偿方程上述方程中的未知混合矩阵H,并估计第j个电机单元的尖峰序列为: \[ \widehat{s}_j(n)=w_j^T \bar{y}(n) \\ w_j=C_{\bar{y} \bar{y}}^{-1} c_{s_j \bar{y}} \] PNR 的计算公式: \[ \mathrm{PNR}_j=10\cdot\log\left(\frac{E(\widehat{s}_j(n)|_{\widehat{s}_j(n)\geq r})}{E(\widehat{s}_j(n)|_{\widehat{s}_j(n)<r})}\right) \] 整个算法流程:

对online估计所做的改进:
将离线阶段中获得的分离向量应用于在线分解仅当离线和在线阶段的信号特性之间保持相似时,才能确保在线阶段中的EMG分解的有效性。比如在信号是静止的情况下。然而,在一般情况下,初始的分离向量是需要持续自适应的。
为了适应非静态条件,文章提出了一种更新策略,在每次识别新的放电时间序列时调整分离向量\(w_j\)的方法,效果如下:
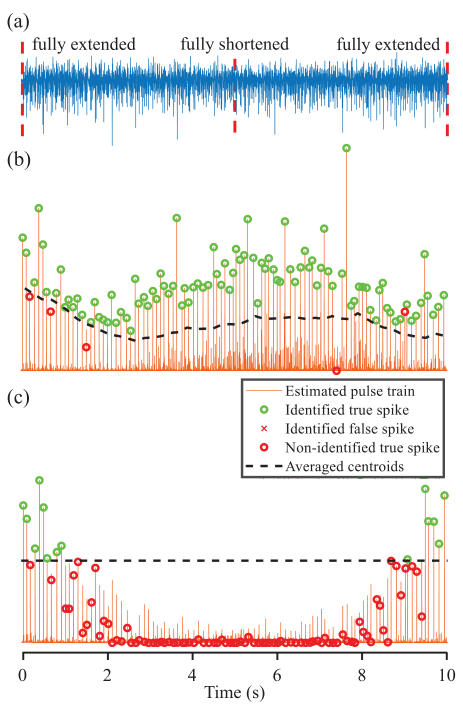
分离向量和聚类中心的更新公式如下: \[ \begin{aligned} &C_{\bar{y}\bar{y}} =C_{\bar{y}\bar{y}}+C_{\triangle\bar{y}\triangle\bar{y}} \\ &c_{s_{j}\bar{y}} =c_{s_j\bar{y}}+\ell\cdot\frac1{card(\Psi_j)}\sum_{n_k\in\Psi_j}\triangle\bar{y}(n_k) \\ &T_{ij}=\frac{w_1T_{ij}+w_2T_{ij}^{^{\prime}}}{w_1+w_2},i=1,2 \end{aligned} \] 这里是对分离向量进行更新,这个更新类似于梯度的更新。协方差矩阵表示的是随机变量之间的相关性(注意:相关系数就是根据协方差计算的)。这里在分段后更新了协方差矩阵,相当于加强了这一小段中随机变量的特性
online 估计的滑动窗口:200 ms
一个新的概念有待了解:尖峰间隔变异性
1.3 实验范式
1.3.1 仿真EMG:
通过把MUST卷积MUAP得到仿真的EMG。在每次仿真中,前10秒的信号用于离线训练,而剩余的60秒信号用于测试在线分解的性能。
数据集1:10%,30%,50%持续兴奋下的数据,持续70s。
In dataset Sim1, three contraction conditions were simulated with different input excitation levels (10%, 30%, or 50%). In this dataset, the input excitation was constant and lasted for 70 s. The number of recruited motor units was 52 (10% excitation), 77 (30%), and 89 (50%).
这说明是通过改变募集 MU 的数目来改变兴奋程度的,一定程度上印证了兴奋之和募集 MU 数目以及发放频率有关,MUAP 的幅值是不会改变的。
数据集2:兴奋首先保持10s(这10s 应该是和数据集1中的兴奋是一致的),然后在60s 内变化,兴奋的水平 3 \(\times\) 4 兴奋的改变速度 \(=\) 12组
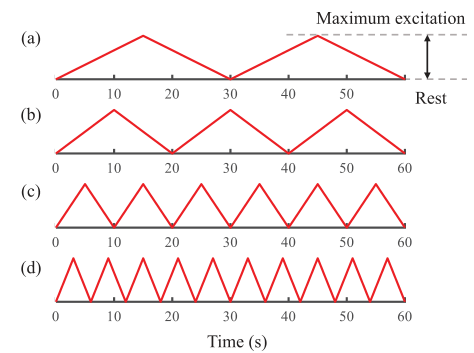
- 数据集3:兴奋的水平是保持不变的,改变MUAP波形(stretching the MUAP duration and compressing the MUAP amplitude )。局限性:保持兴奋不变,意味着发放频率和募集的 MU 数目不变,只改变 MUAP 的形状。
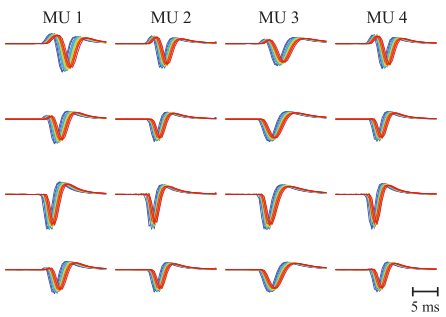
红色和蓝色分别代表肌肉完全伸张和完全收缩情况下的MUAP,可以看到波形虽然有区别,但是是差不多的。
如何量化兴奋程度参考文献:
Models of recruitment andrate coding organization in motor-unit pools
1.3.2 实验数据
真实采集的数据集和模拟仿真的数据集是一一对应的,分为EXP1,EXP2,EXP3。实验数据长40s,前10s用作训练得到分离向量,后30s用作在线分解:
- 在EXP1中,受试者被要求以最大自主收缩(MVC)力的10%、30%和50%的恒定力进行等长抓握
- 在EXP2中,受试者被要求遵循模拟2中描述的力轨迹。为了简化实验,只在三个水平上保持6秒的斜坡
- 在EXP3中,受试者被要求进行非等长动态抓握,抓握周期被设定为6秒。受试者在动态抓握过程中被要求尽量保持收缩水平,但不严格。
从这个实验范式的设置中可以看出:(1)真实的力对应模拟的兴奋水平;(2)通过改变等长收缩来改变MUAP的形状
人数:5——4男1女
设备:
- EMG采集:ELSCH064NM3, 8 × 8 channels, OT Bioelettronica, Italy,3片64通道电极片
- 运动学采集:14通道,5 DT Data Glove 14 Ultra, 5DT Inc. USA
数据预处理:
- 20-500Hz 滤波
- 50Hz 工频干扰及其谐波滤波,梳状滤波器
1.4 分解评估
对于仿真数据集(灵敏度是识别出了多少,准确度是识别出的正确的有多少):
\[
\begin{aligned}
\text { Sensitivity } & =\frac{T P}{T P+F N} \\
\text { Precision } & =\frac{T P}{T P+F P}
\end{aligned}
\] 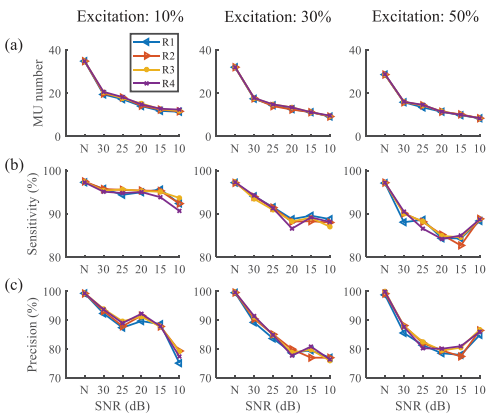
上图是仿真数据集2的分解结果,可以看到随着兴奋程度的增加,分解的MU数目减少,并且时间越长(最左边是30s,最右边是6s),得到的MU数目越多。
对于实验数据:PNR(基于信号的评价标准) \[ \mathrm{PNR}_j=10 \cdot \log \left(\frac{E\left(\left.\widehat{s}_j(n)\right|_{\widehat{s}_j(n) \geq r}\right)}{E\left(\left.\widehat{s}_j(n)\right|_{\widehat{s}_j(n)<r}\right)}\right) \]
1.5 结论
延迟:滑动窗口的计算耗时<50ms,在线分解10s的信号延迟<250ms,
仿真数据集:
在线分解中,sim1的灵敏度和准确度都大于80%
在线分解中,sim1的灵敏度大于80%,准确度大于70%
更新策略在sim1、2中改善不大,但在sim3(对应于动态情形)中对灵敏度和准确度的提升巨大
PNR和sen以及pre之间的回归决定系数
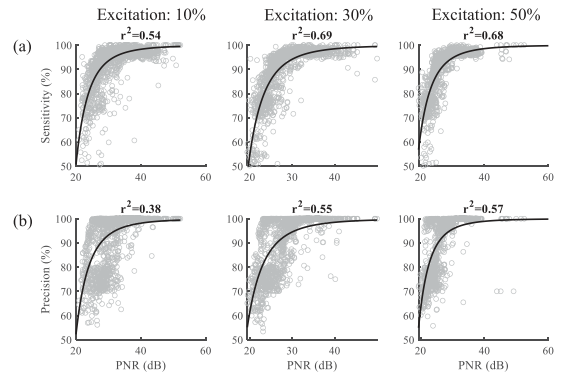
实验数据集:
- 平均PNR为24dB,对应于sensitivity>80%,precision>75%
1.7 分解的条件
等距收缩中的非静态参数来自MU的募集、去募集以及放电频率的变化,这两个参数只影响源信号(?),不影响混合过程,本文提出的更新策略对这种变化是稳健的。
在基于CKC的分解算法中,基于混合过程来计算分离向量。等式中的混合矩阵 H 在等长收缩中是恒定的,但在非等长收缩下随时间变化,这需要相应的分离向量更新。动态非等长收缩中,电极与肌肉的相对位置发生变化,导致MUAP的变化以及混合模式的变化
2. 问题
- 滑动窗口的步长是多少,这篇文章是怎么执行滑动窗口的
文章说延迟250ms,那么推算步长应该是200ms,窗口不重叠
滑动窗口是200ms,但是muap的长度一般就100ms了,是不是窗口里面一个MU只能识别出1个或者0个discharge
这种方法只适用于分解出训练中出现的MU?
使用持续兴奋的数据集得到的分离向量,用在兴奋变化的数据集上,这样吗?