基于盲源分离技术的高密度表面肌电分解

肌电信号分解可以看成是肌电形成的逆过程。肌电分解的主要目的是将肌电信号还原成其基本的组成成分：运动单位动作电位序列（MUAPT）。从而可以将肌电信号中的单个的运动单位识别出来并进行归类，进而得到参与此次肌肉活动的运动单位的个数、种类、发放信息及波形信息。（存疑，是先得到MUAPT？还是MUST） 。尽管FastICA算法非常契合表面肌电信号分解的需求，但FastICA是基于瞬时线性混合模型推导的，而表面肌电信号更符合卷积模型

1.笔记

1.1 改进FastICA及sEMG模型

FastICA的特性与表面肌电分解的需求非常符合 ：

1. FastICA是基于信号的非高斯性来估计源信号。而在肌电信号分解中，源信号运动单位动作电位序列正是稀疏的超高斯信号。这是符合FastICA的理论假设的。也可以说，FastICA是在肌电分解中是利用了运动单位动作电位序列的稀疏性来进行分解的。同时，不同运动单位的发放可以认为是互相独立的，这也符合FastICA 基本假设。
2. 相较于其他独立分量分析方法，FastICA的收敛速度快，鲁棒性更好。并且从迭代方程式来看，FastICA不同于其它基于梯度的优化方法，不需要设置步长参数，这一点给算法的使用带来很大方便。
3. FastICA可以逐个估计源信号。这个的特性是最为重要的。在表面肌电信号分解中，运动单位动作电位叠加十分严重，且运动单位个数未知，信号的信噪比也非常低。要一次性估计出所有运动单位几乎是不可能的任务。而FastICA的这个特性，在探索型数据分析上是十分重要的，它大大简化了求解问题的难度。可以说这是其他大部分盲源分离方法所不具有的优势。

传统的表面肌电模型如下，记为模型A：

$$x_i(t)=\sum_j a_{i j} s_j(t), \quad \text { for } i=1, \cdots, M ; j=1, \cdots, N$$

在这个模型中考虑表面肌电分解的问题, $x_i(t)$ 表示第 $i$ 个通道采集到的表面肌电信号, 而 $s_j(t)$ 则对应着第 $j$ 个运动单位的运动单位动作电位序列。 从该模型中可以看出, 模型假设不同的通道的表面肌电信号是由同样一批运动单位动作电位序列通过不同的权重 $a_{i j}$ 线性叠加得到的。问题就出在这里。 这样的假设意味着, 对每个运动单位来说, 它在不同电极通道中的运动单位动作电位序列的波形是一致的, 所不同的只是波形的幅值大小。这样的假设显然过于简单了, 其并没有考虑到皮肤、脂肪等对动作电位的滤波作用, 也没有考虑运动电位传播到电极处所需要的传播延迟。事实上，由于皮肤和皮下组织的容积导体效应和电极的不同位置的影响，运动单位的波形在每个电极通道中都是各不相同的。

要更为准确地描述表面肌电信号，应该考虑下面这样一个的卷积模型，记为模型B：

$$x_i(t)=\sum_{j=1}^N \sum_{\tau=0}^{L-1} a_{i j}(\tau) s_j(t-\tau) + n(t); \quad i=1,2, \ldots, M$$

在模型 B 中, $a_{i j}$ 和 $s_j(t)$ 的含义都相对模型 A 发生了较为明显的变化，$n(t)$ 是均值为0的高斯白噪声。 $s_{\jmath}(t)$ 从运动单位动作电位序列抽象成了运动单位的发放时间序列。在这里 $s_j(t)$ 是一个0-1序列：

$$s_j(t)=\sum_k \delta\left(t-T_j(k)\right)$$

表示第 $j$ 个运动单位是否在某个时刻 $t$ 发放。 $T_j(k)$ 表示第 $j$ 个运动单位的第 $k$ 次发放时刻, $\delta$ 表示 delta 函数（Dirac Delta Function）。而模型 A 中 $s_j(t)$ 中的波形信息被转移到了 $a_{i j}$ 中, $a_{i j}$ 从叠加权重变成了波形向量。$a_{\imath j}(t), \quad t=0, \cdots, L-1$ 这个向量就代表第 $j$ 个运动单位在第 $i$ 通道中的波形, 波形长度为 $L$, 同时假设对 $\forall k \in N$, 有: $T_j(k+1)-T_j(k)>L$ 。并且对于第 $j$ 个运动单位来说, 其在不同的通道中的波形 $a_{i j}(t)$ 可以是不一样的。简单来说模型 B 的含义便是对某一个通道 $i$ 来说, 第 $j$ 个运动单位的波形与其发放时刻卷积, 就形成了第 $j$ 个运动单位在这个通道中的运动单位动作电位序列, 将所有参与发放的运动单位的运动单位动作电位序列叠加, 就得到该通道采集的表面肌电信号 $x_i(t)$ 。在这个模型中, 有两个假设，这两个假设很重要，涉及到 MUAP 波形的估计：

• 一个是假设在所有通道中, 运动单位的发放时间是一致的。（运动单位一旦发放，其动作电位便会沿着肌纤维传播开来，被各个电极采集到。至于传播延迟，则可以体现在 $a_{i j}(t)$ 偏移量上面。）
• 第二个假设便是每个运动单位在某个通道的波形，在信号持续时间段内是不变的。也就是说这是一个Shift-invariant的系统。第二个假设对于肌电信号来说并不是总成立的。比如在肌肉收缩的过程中肌纤维的长度和运动单位到电极的距离都会发生变化，可能会导致动作电位的形变。因此模型B中可以引入时变的因素从而使得模型更为贴切。但是这同时也会让问题变得更加复杂。就目前来说，肌电信号分解往往只考虑肌肉等长收缩(Isometric Contraction)情况，在这种情况下，肌肉组织并不发生形变，可以认为运动单位动作电位在采集过程中是保持一致的。

表面肌电信号分解最主要的目的就是得到单个运动单位的发放信息和波形信息，其中发放信息最为重要。事实上如果得到了准确的运动单位的发放信息，就不难得到其波形信息(在运动单位持续发放时间足够长的情况下)，比如可以通过发放位置的平均波形来作为运动单位动作电位波形的估计(Spike Trigger Average,STA)。

若是将FastICA直接应用到用卷积模型描述的肌电信号上，效果会十分不好。可以采用扩展矩阵的策略来解决这个问题。事实上，可以将上述卷积混合模型进行扩展，以达到近似解卷积的效果。延迟因子往往根据数据的采样率来确定。一般来说，对于采样率为2kHz的表面肌电信号，K的选择在5个采样点到30个采样点之间会比较合适。

FastICA输出的结果虽然不能直接被当成运动单位动作电位序列，但是它是对应于某个运动单位动作电位序列滤波后的结果，因此可以从FastICA的输出中提取出不同运动单位的发放时间信息。比如，可以认为FastICA输出中波形的峰值位置就对应着某运动单位的发放时刻。

1.2 sEMG模拟过程

运动单位动作电位的波形则由表面肌电模型从单纤维动作电位(SFAP)开始模拟，运动单位的每一根肌纤维在电极处形成的单纤维动作电位进行叠加便是该运动单位在该电极处的运动单位动作电位(MUAP)，运动单位动作电位与该运动单位的发放时间序列卷积，便是运动单位动作电位序列(MUAPT)，这也是肌电分解想要关注的对象。最后所有参与发放的运动单位动作电位序列进行叠加，便得到表面肌电信号。

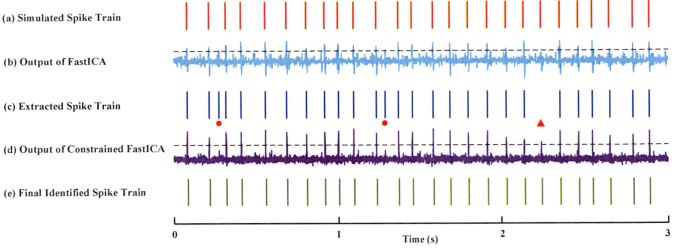
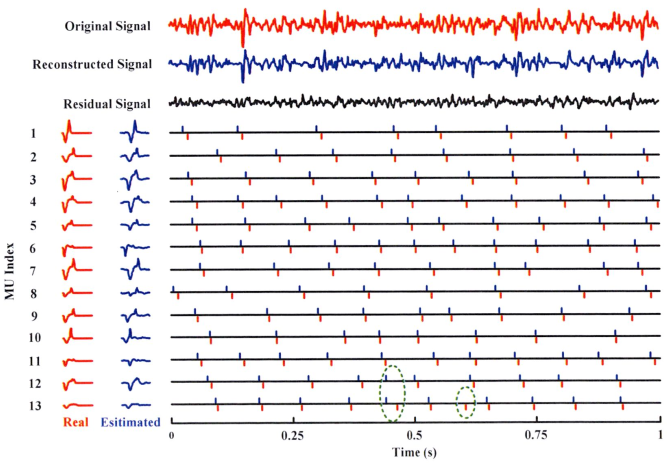
1.3 算法评估

2. Constrained FastICA的不可靠输出

（1）输出不是一个稀疏的发放序列。甚至，它趋向于是一个近似白噪声的序列。这种情况经常是在多次重复的剥离步骤之后算法无法再找到任何新的发放序列下发生的。(这也意味着遇到这种情况时候可以结束分解程序)。

（2）输出仅仅包含若干个离散的尖峰波形。这些少量的尖峰往往并不能认为是一个可靠的运动单位的发放波形。它们通常拥有较大且不规则的发放间隔，并且它们的幅值大小区别往往比较大，并没有很好的一致性。这种情况一般是由于系统噪声引起的，比如采集过程中电极和肌肉之间没有紧密贴合造成的移动伪迹等等。这些尖峰状的噪声往往在大部分通道都具有很大的幅值，并且拥有很强的高斯性，所以它们能轻易地被FastICA识别出来，对运动单位的分解造成干扰 。

（3）输出几乎处处接近于0，除了在某一小段存在一个巨大的单个尖峰或者一一凸起。这往往是FastICA中存在的过度拟合的现象(可能是由于样本数量不足或者该区间段数据存在极强的时间相关性)[98]，又或者就是(2)中提到的一个巨大的移动伪迹。

（4）输出依旧是若干运动单位的发放叠加的结果。如果这些混合的发放最后依旧不能够被Valley．seeking Clustering分开，那么就应该将它们删去 。

为了避免上述的不合理结果，对输出进行限制：