这篇文章通过稀疏度来得到分离向量，而不是FASTICA中的非高斯性和独立性。整个分解算法分为两个迭代过程，第一个迭代过程类似于fastICA，第二个迭代过程类似于CKC。该方法的主要假设是，两个运动单元脉冲序列的叠加总是比单个运动单元的叠加更具可变性（方差更大）。
1.笔记
卷积混合可以表示成扩展向量的线性瞬时混合模型。
卷积混合模型： \[ \underline{\underline{x}}(k)=\sum_{l=0}^{L-1} \underline{\underline{H}}(l) \underline{\underline{s}}(k-l)+\underline{\underline{n}}(k) \\ x_i(k)=\sum_{l=0}^{L-1} \sum_{j=1}^n h_{i j}(l) s_j(k-l)+n_i(k) \\ \underline{\underline{x}}(k) = \left[\begin{array}{c} x_1(k) \\ x_2(k) \\ \vdots \\ x_m(k) \end{array}\right] \] 扩展后的线性瞬时混合模型： \[ \begin{aligned} & \underline{\underline{\tilde{x}}}(k)=\underline{\underline{\tilde{H}}} \underline{\underline{\tilde{s}}}(k)+\underline{\underline{\tilde{n}}}(k) \\ & \underline{\underline{\tilde{s}}}(k)=\left[\tilde{s}_1(k), \tilde{s}_2(k), \ldots, \tilde{s}_n(k)\right]^T \\ & \underline{\underline{\tilde{x}}}(k)=\left[\tilde{x}_1(k), \tilde{x}_2(k), \ldots, \tilde{x}_m(k)\right]^T \\ & \underline{\underline{\tilde{n}}}(k)=\left[\tilde{n}_1(k), \tilde{n}_2(k), \ldots, \tilde{n}_m(k)\right]^T \\ & \tilde{h}_{i j}= {\left[\begin{array}{cccccc} h_{i j}[0] & \cdots & h_{i j}[L-1] & 0 & \cdots & 0 \\ 0 & \ddots & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & h_{i j}[0] & \cdots & h_{i j}[L-1] \end{array}\right] } \\ & \underline{\underline{\tilde{H}}}= {\left[\begin{array}{ccc} \tilde{h}_{11} & \cdots & \tilde{h}_{1 n} \\ \vdots & \ddots & \vdots \\ \tilde{h}_{m 1} & \cdots & \tilde{h}_{m n} \end{array}\right] } \end{aligned} \] 对上述符号的理解就是： \[ \left.\underline{\underline{\tilde{H}}}=\left[\begin{array}{cccc}MUAP_{1,1}(t)&MUAP_{1,2}(t)&\cdots&MUAP_{1,NR}(t)\\\vdots&\vdots&\vdots&\vdots\\MUAP_{NM,1}(t)&MUAP_{NM,2}(t)&\cdots&MUAP_{NM,NR}(t)\end{array}\right.\right] \] 注意，这里的MUAPT是扩展后的MUAPT！
这种分离方法的前提是，需要满足一个条件：\(R \geqslant(n / m) L\)。因此MUAP相对较长的话需要扩展的多一点来满足上述条件。
Currently, the only sufficiently validated method for testing the accuracy of EMG decomposition in the absence of a gold standard provided by expert decomposition, is the comparison of the decomposition results of two or more EMG signal sets that share some common sources (discharge timings) (De Luca et al 2006, Holobar et al 2010, Holobar and Farina 2014), but also have a number of different sources and different action potential shapes.
算法有效性的一种评价方法就是比较分解两套或者多套EMG数据的结果，这些数据必须包含共同的源。
1.1 为什么要扩展？
为了增大观测数和源数之间的比例。
In order to increase the ratio between the number of observations and the number of sources and, thus, conditionality of the described mixing process, the observations are also usually extended, adding R delayed versions of each observation.
扩展要满足一个要求才能用最小二乘法求解： \[ R\geqslant(n/m)L \] 上式中R是扩展的参数，n是源的个数，m是观测的通道数，L是MUAP的长度，这在调参的时候需要注意。
由于源的大多数样本为零，因此可以作为尖峰队列这种特定结构，并且在对源扩展了之后也保持了稀疏性。直观地说，这是由于具有相关激发的源的总和总是不如单个源稀疏，除非激发完全一致（可能性非常小）。
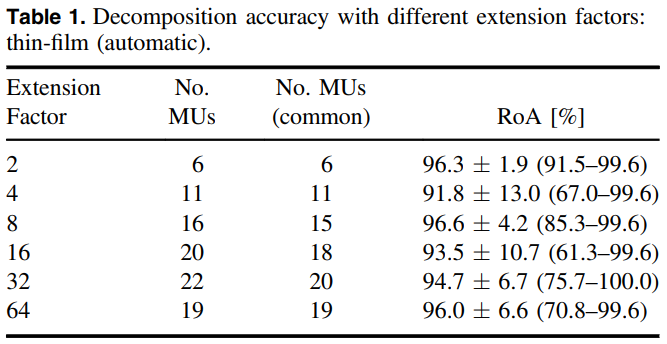
扩展系数与识别到的MU数目之间的关系：
1.2 如何执行分离向量的初始化？
对白化后的矩阵，取一列观测向量，先求和，再求平方，峰值最大处可以视为肌肉的激活程度最高，出现运动单元放电的可能性最大，取该列向量来初始化分离向量。
1.3 为什么要执行白化？
现实世界中的独立信号往往都是非高斯的，而非高斯信号线性混合后的混迭信号会比源信号更趋近于高斯分布（中心极限定理）。因此可以说“非高斯就是独立的”。为此，算法的目标就由直接度量独立性转变为度量输出的非高斯性，也即是需要使得输出的概率密度距离高斯分布最远。Aapo HyVarinen当时提出使用峭度或者负熵来作为非高斯性度量。信息论指出，在方差一定的情况下，高斯变量具有最大的熵，因此负熵的值恒非负，当且仅当p(y)为高斯分布时候其值为0。因此负熵的值越大则意味着该变量的非高斯性就越强。白化的详细原理参考笔记：白化学习笔记
1.4 如何执行白化？
本文中的白化步骤为：
- 对扩展后的矩阵计算协方差
- 对协方差矩阵进行特征值分解
- 计算特征值中最小一半的平均值
- 将小于平均值的特征值替换成平均值
- 根据公式得到白化矩阵
正则化过程是为了减小求解的数值不稳定性（基于假设噪声的方差等于最小一半特征值的均值）。这个值太小会引入部分噪声，影响估计；这个值太大会导致一些源信号被忽略掉。
The coefficient of variation of inter-spike intervals (CVoISI)描述的是相邻脉冲之间的时间间隔的变异系数，这个值应该越小越好。50%以上的MU应该剔除。计算cv时，先对MUST取差分得到间隔，然后用间隔的标准差初一间隔的均值。
Rate of Agreement是指采用两种方法分解，并将结果比较，根据计算公式可以看到，这个值是属于0-1的，越接近1说明两种方法的吻合度越高，分解结果也越可信。当RoA大于30%就可以认为是同一个MU。当two source method不可行时，由于SIL于RoA具有高度的线性关系，因此可以通过计算归一化的SIL来检验分解的有效性。
SIL计算公式： \[ \begin{aligned} & \text{silhouete score}=\frac{b-a}{max(a,b)}\\ & a=inter-cluster\;sum\;of\;point-to-centroid\;distances\\ & b=intra-cluster\;sum\;of\;point-to-centroid\;distances\\ \end{aligned} \] SIL称为轮廓系数，由簇内不相似度a(i) ，簇间不相似度b(i) 计算得来，反应的是聚类的效果，SIL计算代码如下：
1 | intra_sums = sum(abs(noise_cluster - noise_centroid)) + sum(abs(peak_cluster - peak_centroid)); |
contrast function既可以衡量独立性，也可以衡量稀疏性，同一脉冲序列的两个不同延迟的线性混合总是比原始脉冲序列更密集。稀疏度是放电速率的函数：放电速率越大，源的稀疏度越低。
人神经的不应期决定了最小的放电间隔（对应放电频率为30-40 pps）
1.5 聚类评估
本文中将聚类的SIL阈值设置为了0.9。本文中认为SIL虽然与PNR的定义不同，但是都是可靠的，并且SIL能够直接用于RoA的计算。
1.6 伪代码
- 最外层for循环，m次，m为观测通道数
- 第一个while循环，fast ICA
- 第二个while循环，CKC，这个循环是为了移除错误的尖峰
也就是说分解的源最多就是观测的通道数，但这几乎不可能。（有文章是把这个for循环的m次设置成大于通道数的）
2. 算法改进
Any other criteria for stopping the second iteration would also be acceptable. For example, it would be possible to apply the SIL measure to this second iteration (note that this measure would also increase with the number of iterations, being an efficient criterion for determining convergence).